How to Read Multi-class Clasification Dataset Python

Multi-Class Imbalanced Classification

Terminal Updated on January v, 2021

Imbalanced classification are those prediction tasks where the distribution of examples across class labels is not equal.

Most imbalanced classification examples focus on binary classification tasks, notwithstanding many of the tools and techniques for imbalanced classification also directly support multi-class classification issues.

In this tutorial, y'all volition discover how to use the tools of imbalanced nomenclature with a multi-course dataset.

Later on completing this tutorial, you will know:

• About the glass identification standard imbalanced multi-class prediction problem.
• How to use SMOTE oversampling for imbalanced multi-course nomenclature.
• How to utilise cost-sensitive learning for imbalanced multi-class classification.

Kicking-outset your project with my new book Imbalanced Classification with Python, including step-past-step tutorials and the Python source code files for all examples.

Permit's become started.

• Updated Jan/2021: Updated links for API documentation.

Multi-Class Imbalanced Classification
Photograph by istolethetv, some rights reserved.

Tutorial Overview

This tutorial is divided into three parts; they are:

1. Glass Multi-Class Classification Dataset
2. SMOTE Oversampling for Multi-Class Classification
3. Price-Sensitive Learning for Multi-Course Classification

Drinking glass Multi-Class Classification Dataset

In this tutorial, nosotros will focus on the standard imbalanced multi-class classification problem referred to every bit "Drinking glass Identification" or simply "glass."

The dataset describes the chemical properties of glass and involves classifying samples of glass using their chemical properties as ane of vi classes. The dataset was credited to Vina Spiehler in 1987.

Ignoring the sample identification number, at that place are nine input variables that summarize the backdrop of the glass dataset; they are:

• RI: Refractive Index
• Na: Sodium
• Mg: Magnesium
• Al: Aluminum
• Si: Silicon
• K: Potassium
• Ca: Calcium
• Ba: Barium
• Fe: Iron

The chemical compositions are measured as the weight percent in respective oxide.

There are seven types of glass listed; they are:

• Class one: edifice windows (float processed)
• Class 2: building windows (non-float processed)
• Class 3: vehicle windows (float processed)
• Grade 4: vehicle windows (non-bladder candy)
• Class v: containers
• Course 6: tableware
• Class 7: headlamps

Float glass refers to the process used to brand the glass.

There are 214 observations in the dataset and the number of observations in each class is imbalanced. Note that there are no examples for class 4 (non-float processed vehicle windows) in the dataset.

• Class 1: 70 examples
• Course 2: 76 examples
• Class 3: 17 examples
• Class 4: 0 examples
• Class 5: thirteen examples
• Class 6: nine examples
• Class 7: 29 examples

Although there are minority classes, all classes are equally important in this prediction problem.

The dataset can be divided into window glass (classes 1-4) and not-window glass (classes v-seven). In that location are 163 examples of window glass and 51 examples of non-window glass.

• Window Glass: 163 examples
• Not-Window Glass: 51 examples

Some other sectionalization of the observations would be between float processed drinking glass and not-bladder processed drinking glass, in the instance of window glass but. This division is more balanced.

• Float Glass: 87 examples
• Non-Float Glass: 76 examples

You tin learn more about the dataset here:

• Glass Dataset (drinking glass.csv)
• Glass Dataset Description (glass.names)

No need to download the dataset; we will download information technology automatically as function of the worked examples.

Below is a sample of the get-go few rows of the information.

1.52101,13.64,four.49,1.10,71.78,0.06,8.75,0.00,0.00,1 1.51761,xiii.89,three.lx,1.36,72.73,0.48,vii.83,0.00,0.00,1 1.51618,13.53,3.55,1.54,72.99,0.39,vii.78,0.00,0.00,ane 1.51766,13.21,3.69,i.29,72.61,0.57,8.22,0.00,0.00,1 1.51742,13.27,3.62,1.24,73.08,0.55,viii.07,0.00,0.00,1 ...

We can see that all inputs are numeric and the target variable in the last column is the integer encoded class label.

Yous can learn more virtually how to work through this dataset every bit role of a projection in the tutorial:

• Imbalanced Multiclass Classification with the Glass Identification Dataset

At present that we are familiar with the glass multi-grade classification dataset, let's explore how we can use standard imbalanced nomenclature tools with it.

Want to Get Started With Imbalance Classification?

Take my free 7-day email crash course now (with sample code).

Click to sign-up and too get a gratuitous PDF Ebook version of the class.

SMOTE Oversampling for Multi-Form Classification

Oversampling refers to copying or synthesizing new examples of the minority classes so that the number of examples in the minority class ameliorate resembles or matches the number of examples in the majority classes.

Mayhap the nigh widely used approach to synthesizing new examples is called the Constructed Minority Oversampling TEchnique, or SMOTE for brusk. This technique was described by Nitesh Chawla, et al. in their 2002 paper named for the technique titled "SMOTE: Constructed Minority Over-sampling Technique."

Yous can learn more about SMOTE in the tutorial:

• SMOTE for Imbalanced Classification with Python

The imbalanced-learn library provides an implementation of SMOTE that we can utilise that is compatible with the popular scikit-learn library.

First, the library must exist installed. Nosotros tin install it using pip equally follows:

sudo pip install imbalanced-learn

Nosotros tin can confirm that the installation was successful by printing the version of the installed library:

# check version number import imblearn print ( imblearn . __version__ )

Running the example volition impress the version number of the installed library; for instance:

Before we apply SMOTE, let's start load the dataset and confirm the number of examples in each form.

ane two 3 iv v 6 7 8 9 10 11 12 13 14 15 16 17 eighteen 19 20 21 22

# load and summarize the dataset from pandas import read_csv from collections import Counter from matplotlib import pyplot from sklearn . preprocessing import LabelEncoder # define the dataset location url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv' # load the csv file as a information frame df = read_csv ( url , header = None ) information = df . values # split into input and output elements X , y = data [ : , : - 1 ] , information [ : , - 1 ] # characterization encode the target variable y = LabelEncoder ( ) . fit_transform ( y ) # summarize distribution counter = Counter ( y ) for k , 5 in counter . items ( ) : per = five / len ( y ) * 100 print ( 'Class=%d, n=%d (%.3f%%)' % ( one thousand , five , per ) ) # plot the distribution pyplot . bar ( counter . keys ( ) , counter . values ( ) ) pyplot . evidence ( )

Running the instance starting time downloads the dataset and splits it into train and test sets.

The number of rows in each course is then reported, confirming that some classes, such as 0 and 1, take many more than examples (more 70) than other classes, such as 3 and four (less than xv).

Class=0, due north=70 (32.710%) Class=1, northward=76 (35.514%) Class=2, north=17 (7.944%) Class=3, n=thirteen (6.075%) Class=4, n=nine (4.206%) Form=v, n=29 (13.551%)

A bar chart is created providing a visualization of the class breakup of the dataset.

This gives a clearer idea that classes 0 and 1 have many more examples than classes 2, 3, 4 and 5.

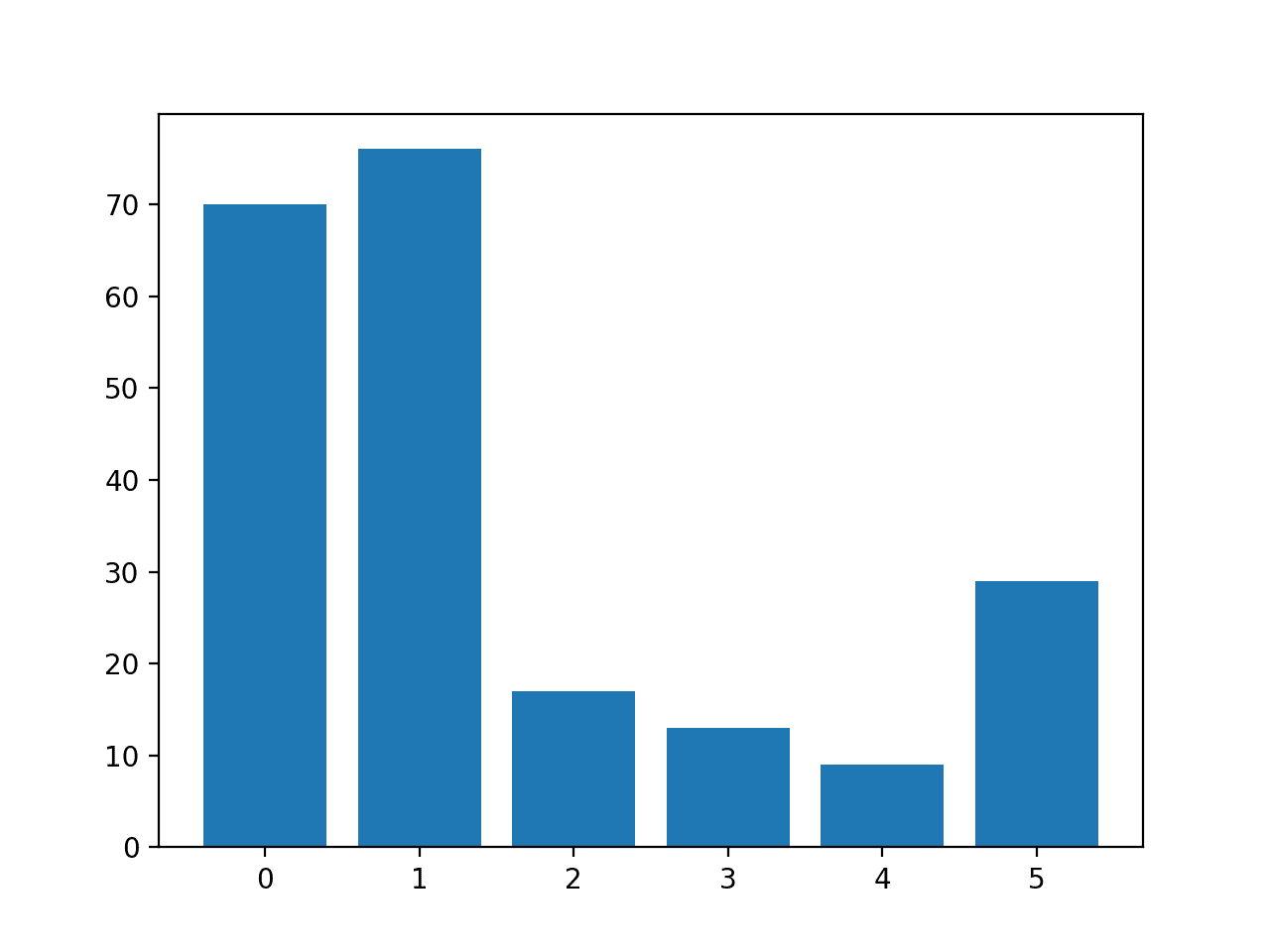
Histogram of Examples in Each Class in the Glass Multi-Grade Nomenclature Dataset

Next, we can apply SMOTE to oversample the dataset.

By default, SMOTE will oversample all classes to have the aforementioned number of examples as the course with the virtually examples.

In this case, class 1 has the most examples with 76, therefore, SMOTE will oversample all classes to have 76 examples.

The complete example of oversampling the glass dataset with SMOTE is listed below.

ane 2 3 4 5 6 7 8 9 10 eleven 12 xiii 14 15 16 17 eighteen nineteen xx 21 22 23 24 25 26

# case of oversampling a multi-class classification dataset from pandas import read_csv from imblearn . over_sampling import SMOTE from collections import Counter from matplotlib import pyplot from sklearn . preprocessing import LabelEncoder # define the dataset location url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv' # load the csv file equally a information frame df = read_csv ( url , header = None ) data = df . values # split into input and output elements X , y = data [ : , : - ane ] , data [ : , - i ] # label encode the target variable y = LabelEncoder ( ) . fit_transform ( y ) # transform the dataset oversample = SMOTE ( ) X , y = oversample . fit_resample ( X , y ) # summarize distribution counter = Counter ( y ) for k , five in counter . items ( ) : per = five / len ( y ) * 100 impress ( 'Class=%d, n=%d (%.3f%%)' % ( k , v , per ) ) # plot the distribution pyplot . bar ( counter . keys ( ) , counter . values ( ) ) pyplot . bear witness ( )

Running the case first loads the dataset and applies SMOTE to it.

The distribution of examples in each class is and then reported, confirming that each form now has 76 examples, as we expected.

Class=0, n=76 (16.667%) Course=ane, north=76 (16.667%) Class=2, northward=76 (sixteen.667%) Class=3, n=76 (sixteen.667%) Course=4, n=76 (16.667%) Class=5, n=76 (xvi.667%)

A bar chart of the course distribution is also created, providing a strong visual indication that all classes now have the aforementioned number of examples.

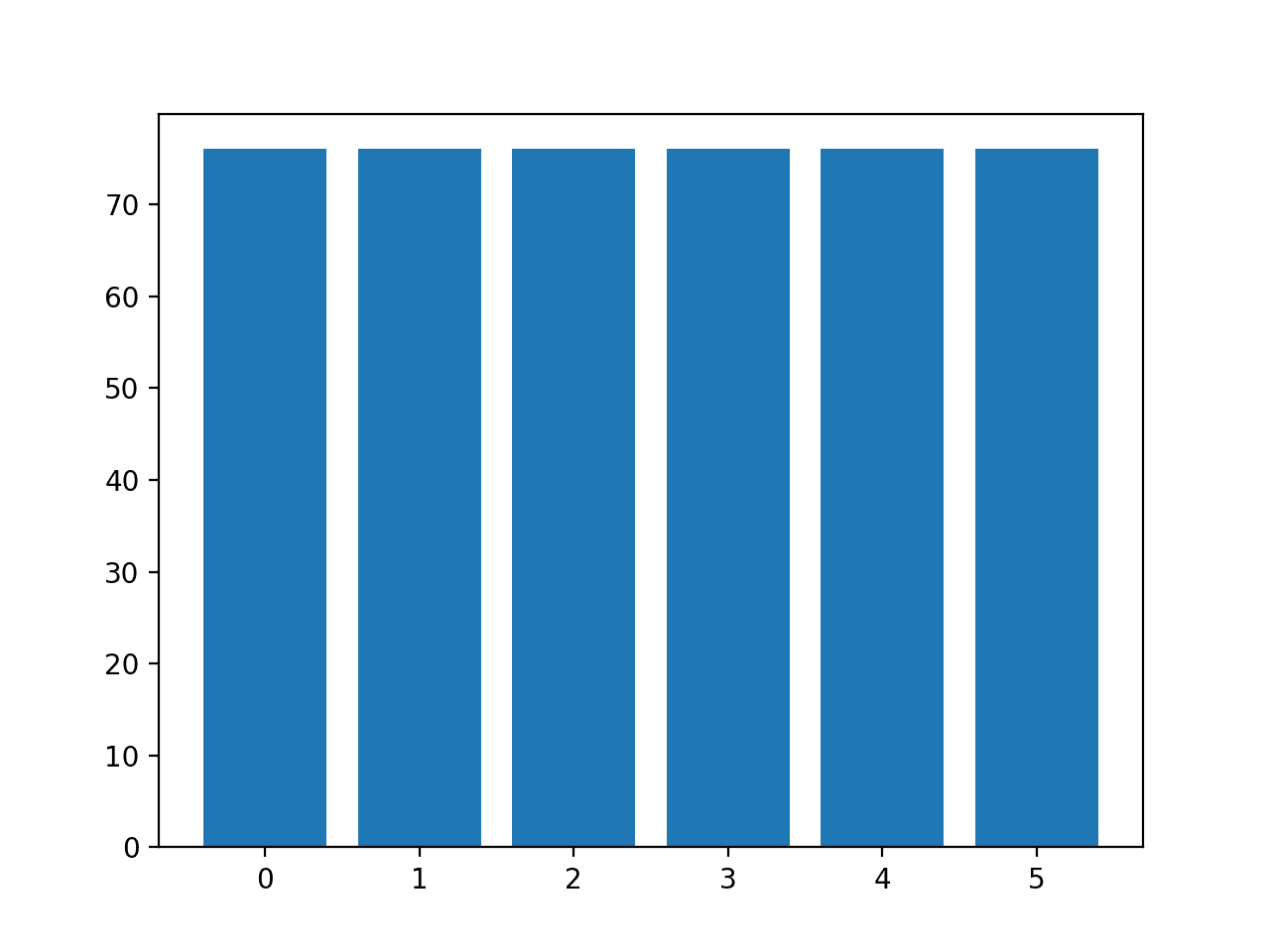
Histogram of Examples in Each Class in the Drinking glass Multi-Class Classification Dataset After Default SMOTE Oversampling

Instead of using the default strategy of SMOTE to oversample all classes to the number of examples in the majority grade, we could instead specify the number of examples to oversample in each class.

For example, we could oversample to 100 examples in classes 0 and ane and 200 examples in remaining classes. This can be achieved by creating a dictionary that maps class labels to the number of desired examples in each class, and so specifying this via the "sampling_strategy" argument to the SMOTE course.

. . . # transform the dataset strategy = { 0 : 100 , 1 : 100 , ii : 200 , 3 : 200 , 4 : 200 , five : 200 } oversample = SMOTE ( sampling_strategy = strategy ) 10 , y = oversample . fit_resample ( X , y )

Tying this together, the complete example of using a custom oversampling strategy for SMOTE is listed beneath.

ane 2 3 4 v 6 7 8 9 ten 11 12 13 fourteen 15 sixteen 17 18 19 20 21 22 23 24 25 26 27

# example of oversampling a multi-grade nomenclature dataset with a custom strategy from pandas import read_csv from imblearn . over_sampling import SMOTE from collections import Counter from matplotlib import pyplot from sklearn . preprocessing import LabelEncoder # define the dataset location url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv' # load the csv file every bit a data frame df = read_csv ( url , header = None ) data = df . values # split into input and output elements X , y = information [ : , : - 1 ] , data [ : , - one ] # characterization encode the target variable y = LabelEncoder ( ) . fit_transform ( y ) # transform the dataset strategy = { 0 : 100 , 1 : 100 , 2 : 200 , 3 : 200 , 4 : 200 , 5 : 200 } oversample = SMOTE ( sampling_strategy = strategy ) X , y = oversample . fit_resample ( X , y ) # summarize distribution counter = Counter ( y ) for k , v in counter . items ( ) : per = 5 / len ( y ) * 100 print ( 'Class=%d, n=%d (%.3f%%)' % ( k , v , per ) ) # plot the distribution pyplot . bar ( counter . keys ( ) , counter . values ( ) ) pyplot . show ( )

Running the instance creates the desired sampling and summarizes the effect on the dataset, confirming the intended upshot.

Course=0, n=100 (10.000%) Class=1, north=100 (10.000%) Grade=two, n=200 (20.000%) Class=iii, due north=200 (20.000%) Form=4, n=200 (xx.000%) Form=v, northward=200 (20.000%)

Note: you may meet warnings that can exist safely ignored for the purposes of this case, such as:

UserWarning: After over-sampling, the number of samples (200) in class 5 will be larger than the number of samples in the majority class (class #i -> 76)

A bar chart of the grade distribution is likewise created confirming the specified grade distribution afterward data sampling.

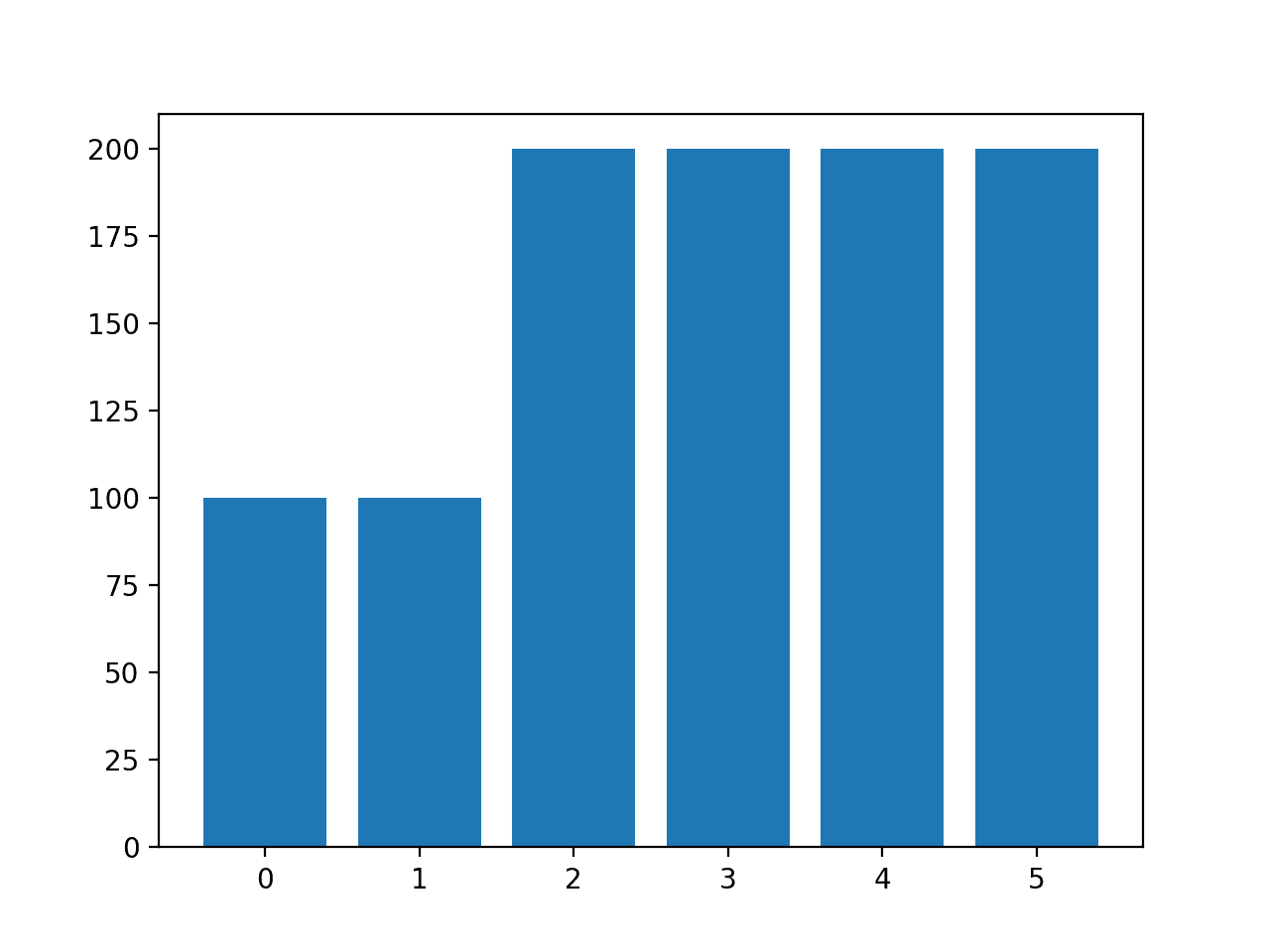
Histogram of Examples in Each Class in the Drinking glass Multi-Class Nomenclature Dataset After Custom SMOTE Oversampling

Note: when using data sampling similar SMOTE, it must merely be applied to the training dataset, not the entire dataset. I recommend using a Pipeline to ensure that the SMOTE method is correctly used when evaluating models and making predictions with models.

You can see an instance of the correct usage of SMOTE in a Pipeline in this tutorial:

• SMOTE for Imbalanced Classification with Python

Cost-Sensitive Learning for Multi-Course Classification

Well-nigh machine learning algorithms assume that all classes have an equal number of examples.

This is non the case in multi-form imbalanced nomenclature. Algorithms can be modified to change the way learning is performed to bias towards those classes that accept fewer examples in the grooming dataset. This is by and large called price-sensitive learning.

For more than on cost-sensitive learning, see the tutorial:

• Cost-Sensitive Learning for Imbalanced Nomenclature

The RandomForestClassifier class in scikit-larn supports price-sensitive learning via the "class_weight" argument.

By default, the random forest form assigns equal weight to each class.

We can evaluate the nomenclature accuracy of the default random forest grade weighting on the glass imbalanced multi-class classification dataset.

The complete case is listed beneath.

1 2 iii 4 v half dozen 7 viii nine ten xi 12 thirteen xiv 15 16 17 xviii nineteen twenty 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

# baseline model and test harness for the drinking glass identification dataset from numpy import mean from numpy import std from pandas import read_csv from sklearn . preprocessing import LabelEncoder from sklearn . model_selection import cross_val_score from sklearn . model_selection import RepeatedStratifiedKFold from sklearn . ensemble import RandomForestClassifier # load the dataset def load_dataset ( full_path ) : # load the dataset as a numpy array data = read_csv ( full_path , header = None ) # recollect numpy assortment data = data . values # split into input and output elements 10 , y = data [ : , : - ane ] , information [ : , - i ] # label encode the target variable to have the classes 0 and 1 y = LabelEncoder ( ) . fit_transform ( y ) return X , y # evaluate a model def evaluate_model ( X , y , model ) : # ascertain evaluation procedure cv = RepeatedStratifiedKFold ( n_splits = 5 , n_repeats = three , random_state = 1 ) # evaluate model scores = cross_val_score ( model , X , y , scoring = 'accuracy' , cv = cv , n_jobs = - one ) render scores # ascertain the location of the dataset full_path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv' # load the dataset X , y = load_dataset ( full_path ) # ascertain the reference model model = RandomForestClassifier ( n_estimators = 1000 ) # evaluate the model scores = evaluate_model ( X , y , model ) # summarize performance print ( 'Mean Accuracy: %.3f (%.3f)' % ( hateful ( scores ) , std ( scores ) ) )

Running the case evaluates the default random forest algorithm with 1,000 trees on the glass dataset using repeated stratified thou-fold cross-validation.

The mean and standard departure classification accuracy are reported at the finish of the run.

Annotation: Your results may vary given the stochastic nature of the algorithm or evaluation procedure, or differences in numerical precision. Consider running the example a few times and compare the boilerplate outcome.

In this instance, we can see that the default model achieved a classification accuracy of nearly 79.vi percent.

Mean Accurateness: 0.796 (0.047)

Nosotros tin can specify the "class_weight" statement to the value "counterbalanced" that will automatically calculates a class weighting that will ensure each form gets an equal weighting during the training of the model.

. . . # define the model model = RandomForestClassifier ( n_estimators = thou , class_weight = 'balanced' )

Tying this together, the consummate example is listed below.

1 2 iii 4 5 6 7 8 9 10 11 12 thirteen fourteen 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

# cost sensitive random woods with default class weights from numpy import hateful from numpy import std from pandas import read_csv from sklearn . preprocessing import LabelEncoder from sklearn . model_selection import cross_val_score from sklearn . model_selection import RepeatedStratifiedKFold from sklearn . ensemble import RandomForestClassifier # load the dataset def load_dataset ( full_path ) : # load the dataset every bit a numpy array data = read_csv ( full_path , header = None ) # remember numpy assortment data = data . values # split into input and output elements X , y = information [ : , : - 1 ] , data [ : , - 1 ] # characterization encode the target variable y = LabelEncoder ( ) . fit_transform ( y ) return 10 , y # evaluate a model def evaluate_model ( X , y , model ) : # define evaluation process cv = RepeatedStratifiedKFold ( n_splits = five , n_repeats = 3 , random_state = ane ) # evaluate model scores = cross_val_score ( model , X , y , scoring = 'accuracy' , cv = cv , n_jobs = - 1 ) render scores # define the location of the dataset full_path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/glass.csv' # load the dataset X , y = load_dataset ( full_path ) # ascertain the model model = RandomForestClassifier ( n_estimators = k , class_weight = 'counterbalanced' ) # evaluate the model scores = evaluate_model ( X , y , model ) # summarize performance print ( 'Hateful Accurateness: %.3f (%.3f)' % ( hateful ( scores ) , std ( scores ) ) )

Running the example reports the hateful and standard departure classification accuracy of the cost-sensitive version of random wood on the glass dataset.

Annotation: Your results may vary given the stochastic nature of the algorithm or evaluation process, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

In this example, nosotros tin see that the default model achieved a lift in classification accuracy over the price-insensitive version of the algorithm, with 80.two per centum classification accuracy vs. 79.half dozen percent.

Mean Accurateness: 0.802 (0.044)

The "class_weight" argument takes a dictionary of class labels mapped to a class weighting value.

Nosotros tin can utilize this to specify a custom weighting, such every bit a default weighting for classes 0 and i.0 that accept many examples and a double class weighting of 2.0 for the other classes.

. . . # define the model weights = { 0 : 1.0 , 1 : 1.0 , 2 : 2.0 , iii : 2.0 , 4 : 2.0 , 5 : 2.0 } model = RandomForestClassifier ( n_estimators = thousand , class_weight = weights )

Tying this together, the complete example of using a custom course weighting for cost-sensitive learning on the drinking glass multi-class imbalanced nomenclature trouble is listed below.

1 2 3 4 v half dozen 7 viii nine x 11 12 13 fourteen fifteen 16 17 18 19 twenty 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

# price sensitive random woods with custom form weightings from numpy import mean from numpy import std from pandas import read_csv from sklearn . preprocessing import LabelEncoder from sklearn . model_selection import cross_val_score from sklearn . model_selection import RepeatedStratifiedKFold from sklearn . ensemble import RandomForestClassifier # load the dataset def load_dataset ( full_path ) : # load the dataset as a numpy array data = read_csv ( full_path , header = None ) # retrieve numpy array data = data . values # split into input and output elements Ten , y = data [ : , : - 1 ] , data [ : , - 1 ] # label encode the target variable y = LabelEncoder ( ) . fit_transform ( y ) render X , y # evaluate a model def evaluate_model ( X , y , model ) : # define evaluation procedure cv = RepeatedStratifiedKFold ( n_splits = 5 , n_repeats = 3 , random_state = one ) # evaluate model scores = cross_val_score ( model , X , y , scoring = 'accuracy' , cv = cv , n_jobs = - 1 ) return scores # define the location of the dataset full_path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/main/glass.csv' # load the dataset X , y = load_dataset ( full_path ) # define the model weights = { 0 : i.0 , 1 : 1.0 , 2 : 2.0 , 3 : 2.0 , four : 2.0 , v : two.0 } model = RandomForestClassifier ( n_estimators = one thousand , class_weight = weights ) # evaluate the model scores = evaluate_model ( X , y , model ) # summarize performance print ( 'Mean Accurateness: %.3f (%.3f)' % ( mean ( scores ) , std ( scores ) ) )

Running the example reports the hateful and standard deviation classification accurateness of the toll-sensitive version of random forest on the glass dataset with custom weights.

Note: Your results may vary given the stochastic nature of the algorithm or evaluation process, or differences in numerical precision. Consider running the example a few times and compare the average outcome.

In this instance, we can see that we achieved a farther lift in accuracy from most eighty.2 percent with balanced class weighting to 80.eight percent with a more than biased class weighting.

Mean Accuracy: 0.808 (0.059)

Further Reading

This section provides more resources on the topic if yous are looking to become deeper.

Related Tutorials

• Imbalanced Multiclass Nomenclature with the Glass Identification Dataset
• SMOTE for Imbalanced Nomenclature with Python
• Cost-Sensitive Logistic Regression for Imbalanced Classification
• Cost-Sensitive Learning for Imbalanced Classification

APIs

• imblearn.over_sampling.SMOTE API.
• sklearn.ensemble.RandomForestClassifier API.

Summary

In this tutorial, you discovered how to use the tools of imbalanced nomenclature with a multi-grade dataset.

Specifically, you learned:

• About the glass identification standard imbalanced multi-class prediction trouble.
• How to apply SMOTE oversampling for imbalanced multi-class nomenclature.
• How to employ toll-sensitive learning for imbalanced multi-course classification.

Practice you lot have any questions?
Ask your questions in the comments below and I volition exercise my all-time to answer.

Go a Handle on Imbalanced Nomenclature!

Develop Imbalanced Learning Models in Minutes

...with simply a few lines of python lawmaking

Discover how in my new Ebook:
Imbalanced Nomenclature with Python

It provides self-study tutorials and end-to-finish projects on:
Performance Metrics, Undersampling Methods, SMOTE, Threshold Moving, Probability Scale, Price-Sensitive Algorithms
and much more...

Bring Imbalanced Classification Methods to Your Machine Learning Projects

See What'due south Within

mcminnstriarthe.blogspot.com

Source: https://machinelearningmastery.com/multi-class-imbalanced-classification/

Share this post